Multiscale and Multiphysics
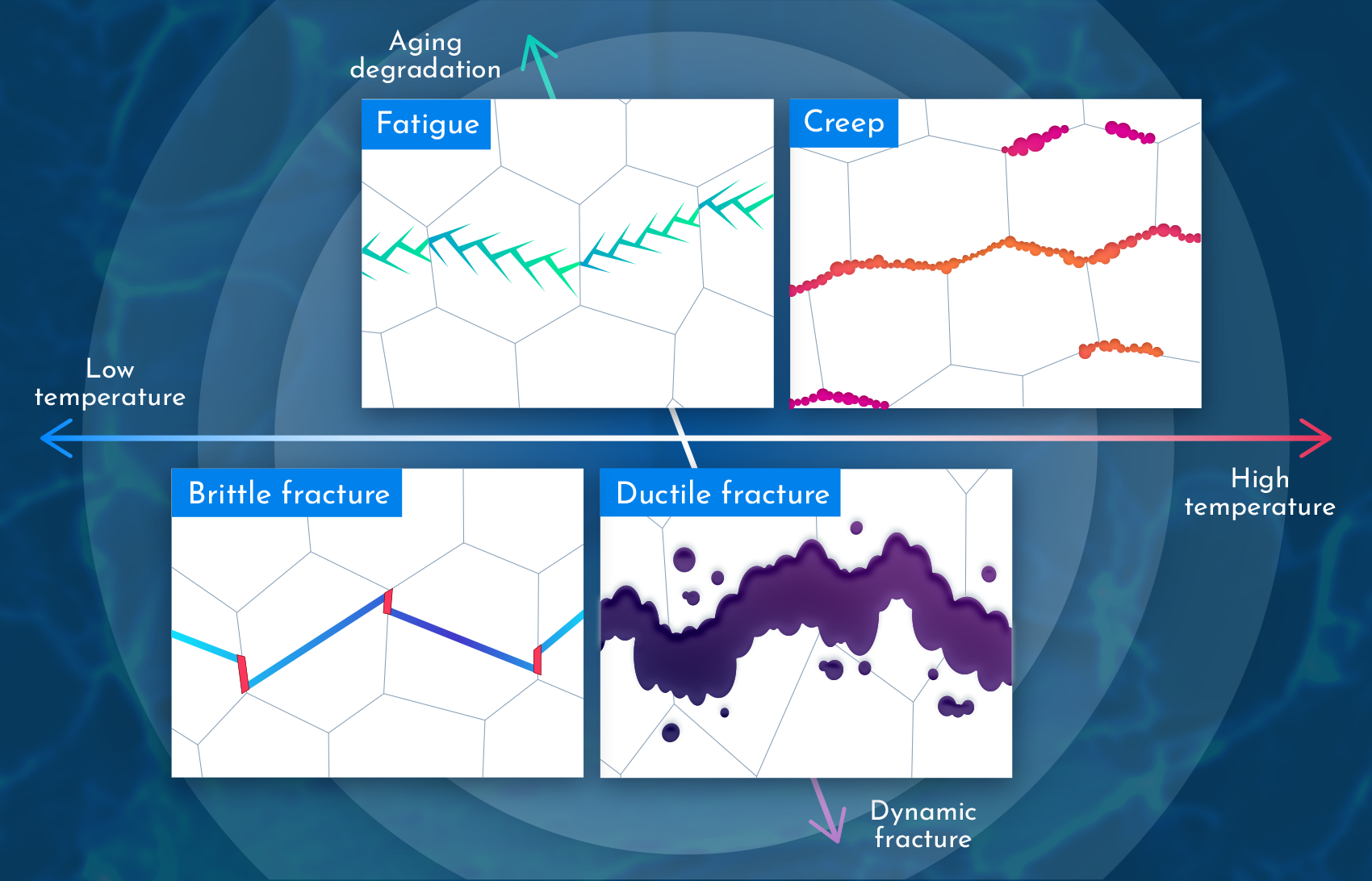
Fractures are complicated. The factors and mechanisms governing fractures arise at different scales, ranging from the macroscopic scale (structural or component level) all the way down to the microscopic scale (grain or atomic level). These factors and mechanisms can even involve physics beyond the mechanics of materials, such as fluid dynamics, thermodynamics, and electromagnetism.
However, developing a model that takes every aspect into consideration is impossible and unnecessary. To guarantee structural integrity, engineers need only appropriately identify the factors and mechanisms that are relevant in each case and integrate them into a reasonable model.
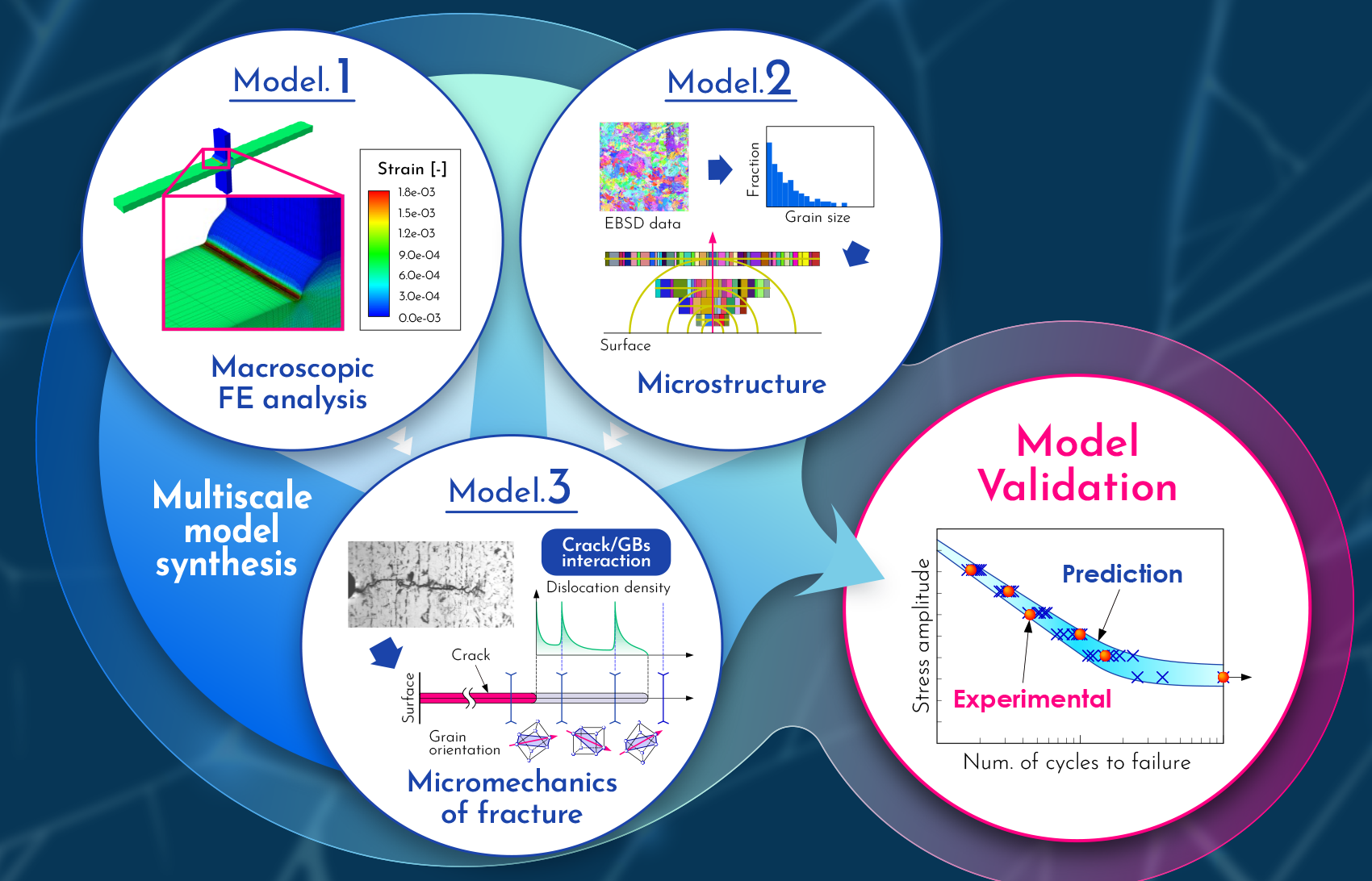
Our group seeks to develop novel methodologies to bridge these governing factors and mechanisms using Multiscale and Multiphysics models. These models will enable us to simulate and explain fracture phenomena in ways that were previously impossible.
Beyond FEM
Finite element method (FEM) is a well-established numerical approach for simulating stress, strain, and deformation in structures using computational mechanics. Though undeniably powerful, FEM was originally designed to simulate mechanical behaviour across a continuum. As a result, it is not entirely suitable for simulating fracture phenomena, especially crack propagation.
Fortunately, there are variations of FEM that are more capable in this domain. The S-version FEM (S-method) can provide high accuracy in arbitrary local positions within a target domain by superposing a finer mesh as needed. Meanwhile, extended FEM (XFEM) uses generalised finite element approximations called “enrichment”, which lets us introduce discontinuities independent of the finite element mesh.
We are currently developing innovative numerical methods Beyond FEM based on these advanced techniques originating from the FEM framework. Our goal is to simulate complicated fracture phenomena accurately, both at the microscale and macroscale.
Verification and Validation
Fractures are so exceptionally complicated that we still have only a very limited understanding of them. In fact, while proposing new models for simulating fractures is not remarkably difficult, it is not enough. What matters is that the model can appropriately explain the actual target phenomenon. Because of this, we prioritize Verification and Validation (V&V) to assess the effectiveness of our models.
Verification involves evaluating the accuracy of the numerical method used, especially in relation to discretization errors. One way to verify a given method is by comparing its results with exact solutions or with reference measurements whose accuracies have already been sufficiently verified. In contrast, validation involves an analysis of the validity of a physics model. This type of evaluation requires comparing the model results with experimental data gathered from actual measurements.